本文主要是解析选择排序算法：直接选择排序和堆排序。
一、直接选择排序
选择排序(Selection sort)是一种简单直观的排序算法。它的工作原理如下。首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。
选择排序的主要优点与数据移动有关。如果某个元素位于正确的最终位置上，则它不会被移动。选择排序每次交换一对元素，它们当中至少有一个将被移到其最终位置上，因此对n个元素的表进行排序总共进行至多n-1次交换。在所有的完全依靠交换去移动元素的排序方法中，选择排序属于非常好的一种。
public static void selectSort(int[] data) { System.out.println("开始排序"); int arrayLength = data.length; // 依次进行n－1趟比较, 第i趟比较将第i大的值选出放在i位置上。 for (int i = 0; i < arrayLength - 1; i++) { // 第i个数据只需和它后面的数据比较 for (int j = i + 1; j < arrayLength; j++) { // 如果第i位置的数据 > j位置的数据, 交换它们 if (data[i] > data[j]) { int tmp = data[i]; data[i] = data[j]; data[j] = tmp; } } System.out.println(java.util.Arrays.toString(data)); } } public static void main(String[] args) { int[] array = new int[10]; for (int k = 0; k < array.length; k++) { array[k] = (int) (Math.random() * 100); } System.out.print("排序之前结果为:"); System.out.println(java.util.Arrays.toString(array)); System.out.println(""); selectSort(array); }
排序结果:
排序之前结果为:[37, 93, 97, 9, 66, 68, 19, 5, 67, 45]开始排序[5, 93, 97, 37, 66, 68, 19, 9, 67, 45][5, 9, 97, 93, 66, 68, 37, 19, 67, 45][5, 9, 19, 97, 93, 68, 66, 37, 67, 45][5, 9, 19, 37, 97, 93, 68, 66, 67, 45][5, 9, 19, 37, 45, 97, 93, 68, 67, 66][5, 9, 19, 37, 45, 66, 97, 93, 68, 67][5, 9, 19, 37, 45, 66, 67, 97, 93, 68][5, 9, 19, 37, 45, 66, 67, 68, 97, 93][5, 9, 19, 37, 45, 66, 67, 68, 93, 97]
算法分析：
（1）关键字比较次数
无论文件初始状态如何，比较次数与关键字的初始状态无关,在第i趟排序中选出最小关键字的记录，需做n-i次比较，因此，总的比较次数为：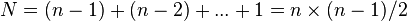
=0(n2)（2）记录的移动次数 当初始文件为正序时，移动次数为0 文件初态为反序时，每趟排序均要执行交换操作，总的移动次数取最大值3(n-1)。 交换次数
，最好情况是，已经有序，交换0次；最坏情况是，逆序，交换
次。交换次数比冒泡排序较少，由于交换所需CPU时间比比较所需的CPU时间多，
值较小时，选择排序比冒泡排序快
二、堆排序
首先，关于堆的概念这里就不说了，详情请看《算法导论》
堆排序的关键在于建堆，下面简单介绍一下建堆的过程：
第1趟将索引0至n-1处的全部数据建大顶（或小顶）堆，就可以选出这组数据的最大值（或最小值）。将该堆的根节点与这组数据的最后一个节点交换，就使的这组数据中最大（最小）值排在了最后。
第2趟将索引0至n-2处的全部数据建大顶（或小顶）堆，就可以选出这组数据的最大值（或最小值）。将该堆的根节点与这组数据的倒数第二个节点交换，就使的这组数据中最大（最小）值排在了倒数第二位。
......
第k趟将索引0至n-k处的全部数据建大顶（或小顶）堆，就可以选出这组数据的最大值（或最小值）。将该堆的根节点与这组数据的倒数第k个节点交换，就使的这组数据中最大（最小）值排在了倒数第k位。
所以我们只是在重复做两件事：
- 1：建堆
- 2：拿堆的根节点和最后一个节点交换
下面通过一组数据说明：
9,79,46,30,58,49
1:先将其转换为完全二叉树，如图
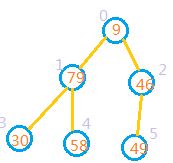
2：完全二叉树的最后一个非叶子节点，也就是最后一个节点的父节点。最后一个节点的索引为数组长度len-1，那么最后一个非叶子节点的索引应该是为(len-1)/2.也就是从索引为2的节点开始，如果其子节点的值大于其本身的值。则把他和较大子节点进行交换，即将索引2处节点和索引5处元素交换。交换后的结果如图：
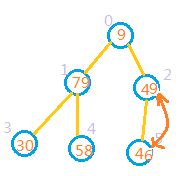
建堆从最后一个非叶子节点开始即可
3：向前处理前一个节点，也就是处理索引为1的节点，此时79>30,79>58,因此无需交换。
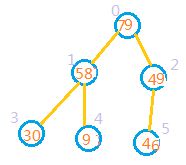
4：向前处理前一个节点，也就是处理索引为0的节点，此时9<79,9<49,因此无需交换。应该拿索引为0的节点与索引为1的节点交换，因为79>49.如图
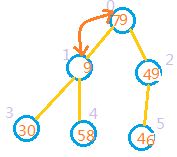
5：如果某个节点和它的某个子节点交换后，该子节点又有子节点，系统还需要再次对该子节点进行判断。如上图因为1处，3处，4处中，1处的值大于3,4出的值，所以还要交换。
算法实现：
public class HeapSort { public static void heapSort(int[] data) { System.out.println("开始排序"); int arrayLength = data.length; // 循环建堆 for (int i = 0; i < arrayLength - 1; i++) { // 建堆 builMaxdHeap(data, arrayLength - 1 - i); // 交换堆顶和最后一个元素 swap(data, 0, arrayLength - 1 - i); System.out.println(java.util.Arrays.toString(data)); } } // 对data数组从0到lastIndex建大顶堆 private static void builMaxdHeap(int[] data, int lastIndex) { // 从lastIndex处节点（最后一个节点）的父节点开始 for (int i = (lastIndex - 1) / 2; i >= 0; i--) { // k保存当前正在判断的节点 int k = i; // 如果当前k节点的子节点存在 while (k * 2 + 1 <= lastIndex) { // k节点的左子节点的索引 int biggerIndex = 2 * k + 1; // 如果biggerIndex小于lastIndex，即biggerIndex + 1 // 代表的k节点的右子节点存在 if (biggerIndex < lastIndex) { // 如果右子节点的值较大 if (data[biggerIndex] < data[biggerIndex + 1]) { // biggerIndex总是记录较大子节点的索引 biggerIndex++; } } // 如果k节点的值小于其较大子节点的值 if (data[k] < data[biggerIndex]) { // 交换它们 swap(data, k, biggerIndex); // 将biggerIndex赋给k，开始while循环的下一次循环， // 重新保证k节点的值大于其左、右子节点的值。 k = biggerIndex; } else { break; } } } } // 交换data数组中i、j两个索引处的元素 private static void swap(int[] data, int i, int j) { int tmp = data[i]; data[i] = data[j]; data[j] = tmp; } public static void main(String[] args) { int[] array = new int[10]; for (int k = 0; k < array.length; k++) { array[k] = (int) (Math.random() * 100); } System.out.print("排序之前结果为:"); System.out.println(java.util.Arrays.toString(array)); System.out.println(""); heapSort(array); }}
排序结果：
排序之前结果为:[18, 14, 33, 42, 2, 63, 62, 97, 94, 63]开始排序[2, 94, 63, 42, 63, 33, 62, 18, 14, 97][14, 63, 63, 42, 2, 33, 62, 18, 94, 97][14, 42, 63, 18, 2, 33, 62, 63, 94, 97][14, 42, 62, 18, 2, 33, 63, 63, 94, 97][14, 42, 33, 18, 2, 62, 63, 63, 94, 97][2, 18, 33, 14, 42, 62, 63, 63, 94, 97][14, 18, 2, 33, 42, 62, 63, 63, 94, 97][2, 14, 18, 33, 42, 62, 63, 63, 94, 97][2, 14, 18, 33, 42, 62, 63, 63, 94, 97]